News
Ehrendoktorwürde für Physiker Prof. Dr. Dieter Vollhardt
Prof. Dr. Dieter Vollhardt wurde vergangene Woche mit der Ehrendoktorwürde der Universität Warschau ausgezeichnet. Gewürdigt wurden damit die wissenschaftlichen Leistungen des emeritierten Physik-Professors der Universität Augsburg sowie seine langjährige enge Zusammenarbeit mit theoretischen Physikerinnen und Physikern der Universität Warschau.

Leuchtturm der quantenmechanischen Forschung
Anfang der 1990er Jahre wurde an der Universität Augsburg das Zentrum für Elektronische Korrelationen und Magnetismus (EKM) ins Leben gerufen. Seitdem hat es sich zu einer Top-Adresse für dieses wichtige Teilgebiet der quantenmechanischen Forschung entwickelt. Das hat kürzlich ein Treffen des wissenschaftlichen Beirats international führender Experten bestätigt.

Feenberg Medal für Augsburger Physiker
Dem theoretischen Physiker Dieter Vollhardt wurde in den USA die "2022 Feenberg Memorial Medal" verliehen. Vollhardt, ehemaliger Inhaber des Lehrstuhls für Theoretische Physik III/Elektronische Korrelationen und Magnetismus am Institut für Physik der Universität Augsburg, erhielt die hohe Auszeichnung zusammen mit Antoine Georges (Frankreich) und Gabriel Kotliar (USA).

Fundamentale Frage der Quantenphysik
Ein internationales Team von Physikern unter Beteiligung der Universität hat erstmals eine wichtige theoretische Vorhersage der Quantenphysik bestätigt. Die Berechnungen dazu sind so komplex, dass sie bislang selbst Supercomputer überforderten. Den Forschern gelang es jedoch, sie mit Methoden aus dem Bereich der künstlichen Intelligenz deutlich zu vereinfachen.

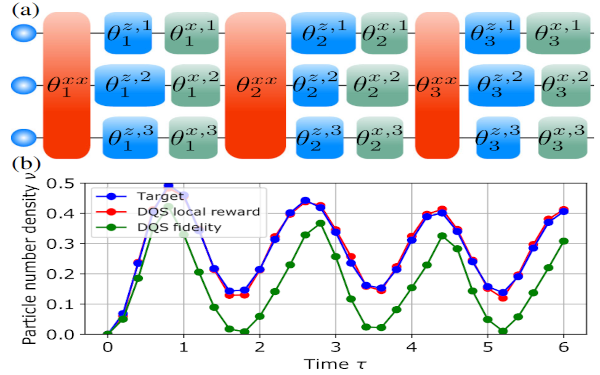
Paper: Reinforcement Learning for Digital Quantum Simulation
Digital quantum simulation on quantum computers provides the potential to simulate the unitary evolution of any many-body Hamiltonian with bounded spectrum by discretizing the time evolution operator through a sequence of elementary quantum gates. A fundamental challenge in this context originates from experimental imperfections, which critically limits the number of attainable gates...
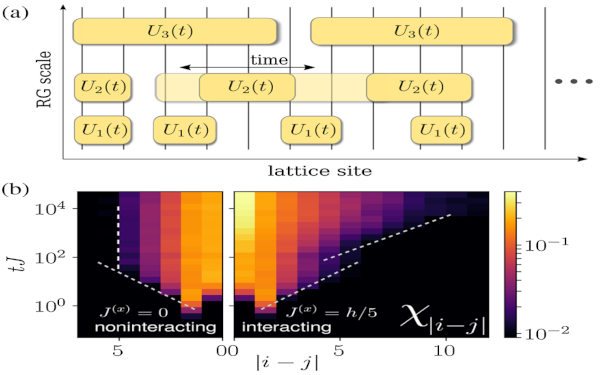
Paper: Unitary Long-Time Evolution with Quantum Renormalization Groups and Artificial Neural Networks
In this work, we combine quantum renormalization group approaches with deep artificial neural networks for the description of the real-time evolution in strongly disordered quantum matter. We find that this allows us to accurately compute the long-time coherent dynamics of large many-body localized systems in nonperturbative regimes including the effects of many-body resonances.
Allgemeine Kontaktinformationen:
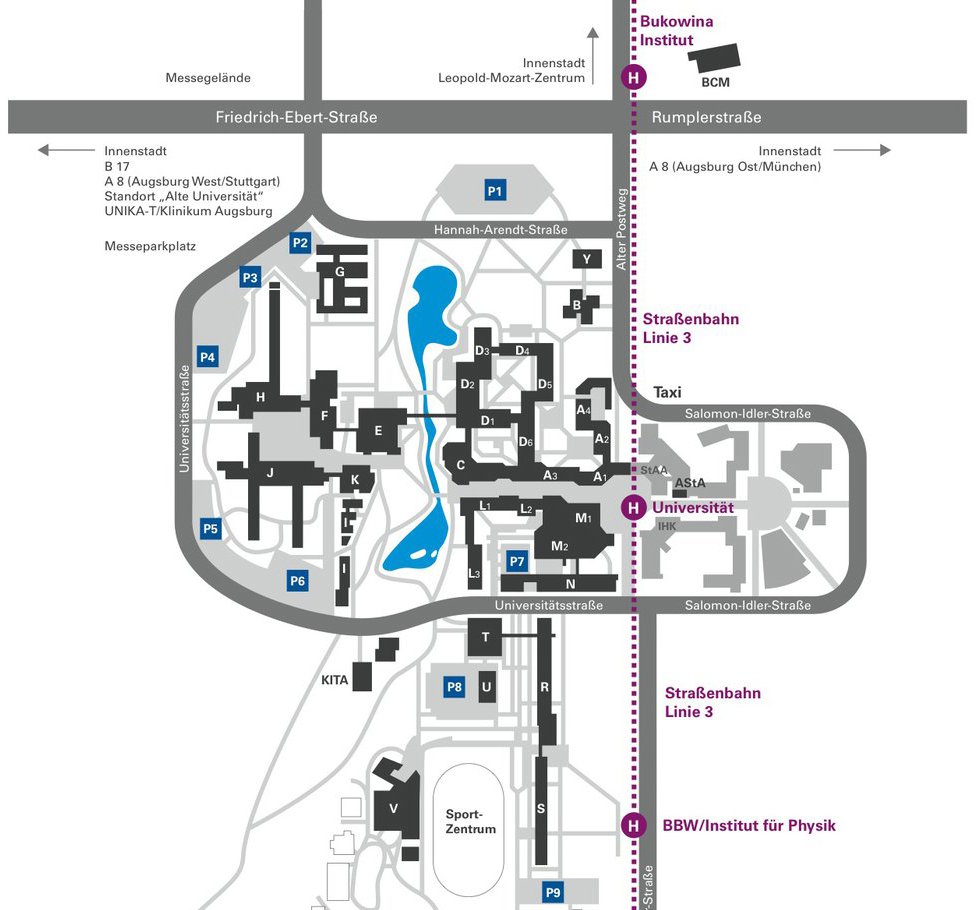
Anschrift: Universitätsstraße 1 (Physik Süd), 86159 Augsburg
Telefon: +49-(0)-821-598-3701 (Sekretariat)
Fax: +49-(0)-821-598-3725
E-Mail: angelika.abendroth@physik.uni-augsburg.de
Gebäude/Raum: 410 (S)