Experimentalphysik V
Lehrstuhl Neuigkeiten

Universalitäten bei der Glasbildung
In einem kürzlich erschienenen Beitrag im führenden physikalischen Fachjournal "Nature Physics" berichten PD Dr. Peter Lunkenheimer und Prof. Dr. Alois Loidl zusammen mit Kollegen aus Göttingen, Berlin und Mailand über unerwartet universelle Beziehungen zwischen der thermischen Ausdehnung und der Glasübergangstemperatur von glasbildenden Materialien, was neue Einblicke in die komplexe Natur des Glasübergangs gewährt.
Obwohl Gläser zu den ältesten vom Menschen genutzten Materialien gehören, sind die mikroskopischen Vorgänge beim Übergang eines Glases in die Flüssigkeit (oder umgekehrt) noch weitgehend unverstanden. Durch die Analyse der thermischen Ausdehnung und der Glasübergangstemperatur von mehr als 200 Gläsern und Flüssigkeiten konnten die Physiker nun nachweisen, dass die Verflüssigung von Gläsern wesentlich dadurch bestimmt wird, dass die Bewegung der Atome oder Moleküle in der glasbildenden Flüssigkeit typischerweise "kooperativ", d.h. gemeinsam, erfolgt. Dies kann den Energieaufwand für die Glasverflüssigung deutlich erhöhen. Zudem finden die Forscher eine weitere überraschend universelle Korrelation: Die thermische Ausdehnung im flüssigen Zustand ist universell um etwa einen Faktor 3 größer als im Glaszustand eines Materials, obwohl die Ausdehnung in beiden Materialzuständen eigentlich von grundsätzlich verschiedenen Mechanismen bestimmt sein sollte.
Insgesamt tragen die gefundenen Universalitäten wesentlich zu einem tieferen Verständnis von so unterschiedlichen glasbildenden Materialien wie silikatbasierten Alltagsgläsern, Polymeren und metallischen Gläsern bei.
Mehr Infos (Pressenmitteilung der Universität Augsburg)

Geladene ferroelektrische Domänenwände als Schaltelement für die Nanoelektronik
Domänenwände für die Nanoelektronik
Ferroelektrische Domänenwände sind im Forschungsfokus der Nanoelektronik für „schlanke“ Bauteile. Die elektronisch funktionalen Wände erlauben es miniaturisierte Komponenten für Schaltkreise, wie Schalter, Dioden oder Kondensatoren, in einem „einzigen“ Material zu designen.
Die neuesten Forschungsergebnisse der Forschungskooperation zwischen Physikern und Materialwissenschaftlern der Universität Augsburg und der Norwegian University of Science and Technology (NTNU) in Trondheim zeigen nun auch, dass, so Prof. Dr. Dennis Meier „neben klassischen DC (direct current) Komponenten auch AC (alternating current) Bauteile, wie Thyrectoren oder Dioden mit funktionalen Wänden realisiert werden können.“ Dies stellt so nach PD Dr. Stephan Krohns „einen wichtigen Schritt dar, um eine Verbindung zwischen aktiven und passiven Komponenten mit diesen ferroelektrischen Domänenwände zu erstellen.
Neue Messmethode
Zu diesen Erkenntnissen gelangte das internationale Team durch Untersuchungen an dem hexagonalen Manganat ErMnO3 mithilfe der erst kürzlich entwickelten Mikroskopie Methode AC-cAFM. „Es handelt sich hierbei um eine Weiterentwicklung der Standard-Mikroskopie-Technik Conductive Atomic Force Microscopy, bei der eine AC Spannung an die Probe angelegt wird, während das zur DC Komponente gehörende Stromsignal gemessen wird.“ berichtet Dr. Jan Schultheiß. „Durch Kombination spannungsabhängiger spektroskopischer Messungen auf makroskopischer und lokaler Skala zeigen wir ein ausgeprägtes nicht-lineares Verhalten am Elektroden-Wand-Übergang, das mit dem Domänenwand-Ladungszustand korreliert.“ berichtet Lukas Puntigam.
Vielseitige Anwendungsbereiche
Die Arbeit „Charged Ferroelectric Domain Walls for Deterministic ac Signal Control at the Nanoscale“ erschien kürzlich im Journal Nano Letters. Basierend auf diesen Ergebnissen scheinen vielseitige Anwendungsbereiche für Domänenwände für elektronische AC Bauelemente im Kilo- bis Megahertz Bereich möglichen zu werden. Dies stellt einen weiteren wichtigen Schritt in der Charakterisierung der elektronischen Eigenschaften und ihrer Transportphänomene in ErMnO3 im Hinblick auf das Anwendungsgebiet der Nanoelektronik dar.
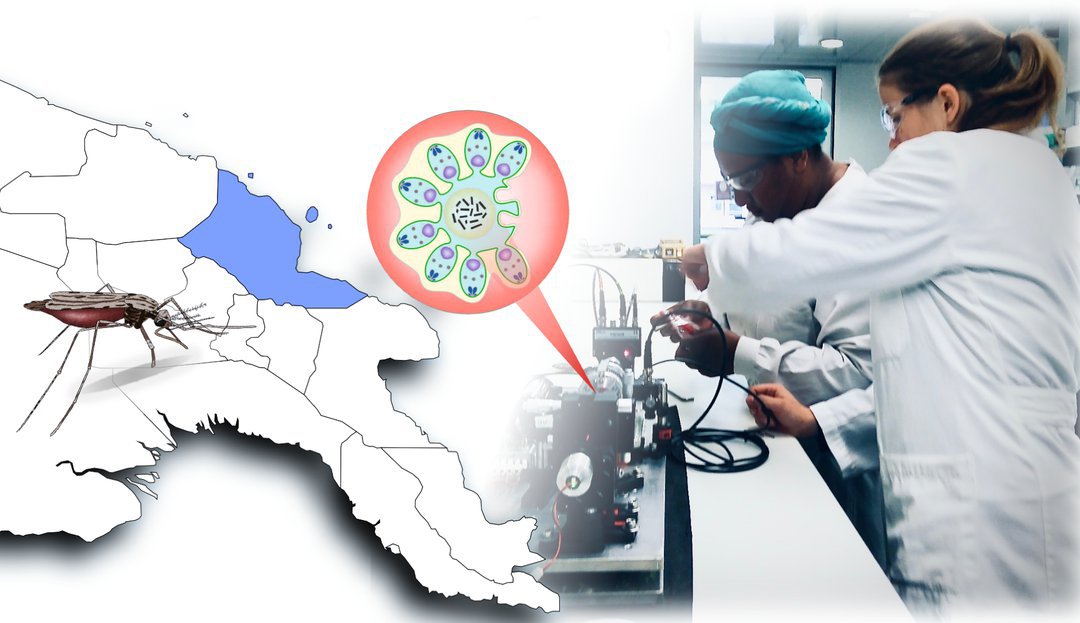
Malaria: Physiker entwickeln neue Diagnose-Methode
„Augsburg/FL/MH – Physiker der Universität Augsburg haben mit Kollegen von der australischen James Cook University eine neue Diagnose-Methode auf Malaria entwickelt. In einer Feldstudie in Papua-Neuguinea haben sie das Verfahren nun an rund 1000 Personen getestet. Demnach ist es ähnlich treffsicher wie etablierte Ansätze und zugleich sowohl kostengünstig als auch einfach in der Handhabung. Die Studie ist nun im renommierten Fachjournal Nature Communications erschienen.“

KI bringt Materialforschung für Nanoelektronik voran
„Die zukünftige Elektronik benötigt miniaturisierte und multifunktionale elektronische Bauteile, die ohne komplexe Materialkombinationen realisiert werden können. Domänenwände stehen hierbei im Fokus der Materialforschung, da diese Wände Grenzflächen auf Nanometerskala zwischen Bereichen gleichmäßiger Orientierungen, z.B. ferroelektrische Polarisation, darstellen.“
Mehr Infos

Projekt „Pawsthesis“
„Augsburg/BB – Wenn dem „besten Freund des Menschen“ eine Pfote oder gar ein ganzes Bein fehlt, ist das eine Qual für Tier – und auch für die Halter. Zwei Studierende der Universität Augsburg entwickeln im Rahmen des Projekts „Pawsthesis“ Prototypen von Beinprothesen. Dies könnte mittelfristig eine gute Lösung für derart gehandicapte Hunde werden.“
Mehr Infos

Dielektrische Ordnung von Wassermolekülen in einem dipolaren Gitter
In einem kürzlich erschienen Artikel in "Nature Communications" lösen wir zusammen mit Forschern aus Moskau, Novosibirsk, Prag und Stuttgart eine alte Streitfrage: Können die dipolaren Wassermoleküle sich spontan parallel anordnen und damit einen ferroelektrischen Zustand ausbilden? Solch eine exotische Form von Wasser wird als hochrelevant für verschiedene natürliche Systeme angesehen und könnte zudem zukünftige Anwendungen in biokompatibler Nanoelektronik ermöglichen. Mit einer Kombination verschiedener Experimente konnten wir zusammen mit unseren Kollegen nachweisen, dass Wassermoleküle, die in nanometergroßen Kanälen innerhalb eines Kristalls aus der Beryll-Familie eingeschlossen sind, tatsächlich einen solchen Zustand ausbilden können.
Mehr Infos

Macroscopic manifestation of domain-wall magnetism and magnetoelectric effect in a Néel-type skyrmion host
Geometrical or dimensional constraints can promote the formation of new quantum phases which are absent in bulk systems. Such constraints can be imposed naturally via mesoscale domain patterns or topological defects on the atomic scale. By combination of detailed magnetoelectric and magnetic torque measurement and supported by neutron scattering and real space imaging experiments we found an additional magnetic state in Skyrmion host material GaV4Se8 which emerges at polar domain walls. A clear anomaly in the magneto-current indicates that the DW confined magnetic states also have strong contributions to the magnetoelectric response. We expect polar domain walls to commonly host such confined magnetic edge states and, thus, offer a fertile ground to explore novel forms of magnetism.

Magnetoelektrische Spektroskopie der Spin Anregungen in LiCoPO4
Die magnetoelektrische Spektroskopie ist eine kraftvolle berührungslose Methode für die Bestimmung aller off-diagonalen Elemente des magnetoelektrischen Tensors. Unsere Kollegen demonstrieren die Wikrsamkeit dieser optischen Methode durch die Messung der off-diagonalen magnetoelektrischen Antwort von LiCoPO4 in dem GHz-THz Bereich. Nach ihrer Erfindung ist die magnetoelektrische Wirkung in diesem Antiferromagnet vom symmetrischen (quadrupolaren) Teil des magnetoelektrischen Tensors dominiert.

Ferroelektrizität in vektorchiralen Phasen
Die Chiralität, d.h. die Händigkeit von Objekten ist für viele Bereiche der Biologie und der Chemie von großer Bedeutung. Aber auch für physikalische Phänomene spielt Chiralität, z.B. bei Symmetrieaspekten in frustrierten Magneten, eine wesentliche Rolle. Bei nichtkollinearen magnetischen Grundzuständen können Spin-Spiralen auftreten. Für diese ist vorhergesagt, dass sogar oberhalb der magnetischen Ordnungstemperatur sogenannte vektorchirale Phasen auftreten, bei denen die Drehrichtung (entweder im Uhrzeigersinn oder gegen den Uhrzeigersinn) zwischen benachbarten Spins geordnet wird, jedoch keine explizite Winkelbeziehung zwischen benachbarten Spins besteht. Mittels magnetfeldabhängiger Polarisationsmessungen liefern wir erstmals den Beweis für das Auftreten dieses Phänomens in LiCuVO4, einem eindimensionalen Quantenmagneten mit konkurrierenden ferromagnetischen und antiferromagnetischen Wechselwirkungen (im gezeigten Phasendiagramm mit "VC" bezeichnet). Dieser Nachweis beruht darauf, dass der vektorchirale Zustand eine endliche ferroelektrische Polarisation bei Temperaturen oberhalb der dreidimensionalen Ordnung der Spin-Spirale impliziert.

Optisches Pumpen der magnetischen Skyrmionen
GaV4S8 ist ein multiferroischer Halbleiter, der magnetische Zykloiden- (Cyc) und Néel-Typ Skyrmionengitter (SkL) Phasen in einem thermisch und magnetisch weiten Stabilitätsbereich aufweist. Wir untersuchen die kohärente Generierung kollektiver Spinanregungen in den Zykloiden- und Skyrmionenphasen mithilfe zeitaufgelöster magnetooptischer Kerr Spektroskopie. Nach unseren mikromagnetischen Simulationen sind diese Anregungen durch eine optisch induzierte Modulation der uniaxialen Anisotropie geführt. Unsere Ergebnisse strahlen die Spindynamik in anisotropischen Skyrmionenträger Materialien an und ebnen einen neuen Weg der optischen Manipulation ihrer magnetischen Ordnung.
Forschungsthemen
Die in unserer Arbeitsgruppe durchgeführten Untersuchungen decken ein weites Feld der Physik der kondensierten Materie ab. Unser besonderes Interesse gilt neuen Materialien für zukünftige Anwendungen in der Elektronik, unkonventionellen Grundzuständen, Supraleitern und der Dynamik ungeordneter und biologischer Materie.



Experimentelle Methoden
Neben einer großen Anzahl von Methoden zur Probencharakterisierung ist die Kombination verschiedener spektroskopischer Methoden eine weitere Stärke unserer Gruppe. Dies erlaubt tiefe Einsichten in die mikroskopischen Eigenschaften kondensierter Materie. Diese Methoden umfassen nicht nur dielektrische, THz und optische Spektroskopie sondern auch Elektronenspin- und Kernspinresonanz-Methoden.



Nationale und Internationale Kollaborationsprojekte
Unsere Arbeitsgruppe nimmt an verschiedenen speziell geförderten regionalen, nationalen und internationalen Kollaborationsprojekten teil:

Sino-German Cooperation on Emergent Correlated Materials
Das Chinesisch-Deutsche Zentrum für Wissenschaftsförderung (CDZ) finanziert ein von den Universitäten Zhejiang (Hangzhou) und Augsburg geleitetes Kooperationsprojekt chinesischer und deutscher Forschungsinstitute über elektronisch hochkorrelierte Materialien.
Ansprechpartner
Allgemeine Kontaktinformationen:
Anschrift (Sekretariat):
Christine Mayr
(Raum 308, Ebene 3)
Universitätsstrasse 1
D-86159 Augsburg
Deutschland
Telefon: +49 821 598 -3602
Fax: +49 821 598 -3649
E-Mail: christine.mayr@uni-a.de
Postadresse:
Experimentalphysik V
Institut für Physik
Universität Augsburg
Universitätsstrasse 2
D-86135 Augsburg
Deutschland
Lieferadresse:
Experimentalphysik V
Institut für Physik
Universität Augsburg
Universitätsstrasse 1
D-86159 Augsburg
Deutschland
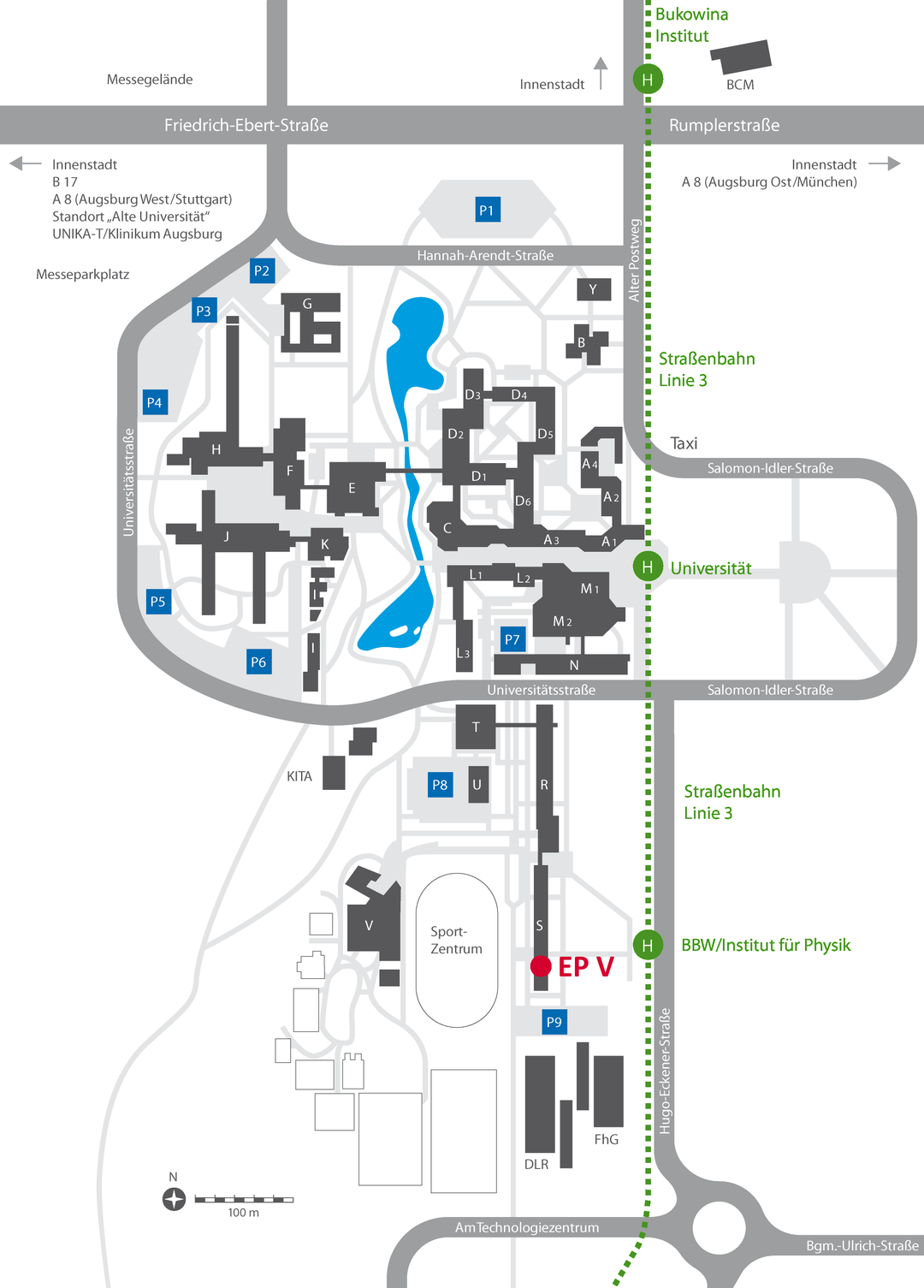
Anfahrt:
Der Lehrstuhl für Experimentalphysik V befindet sich im Gebäude S des Instituts für Physik der Universität Augsburg. Das Sekretariat befindet sich in Ebene 3 im Raum 308.
Anreise mit öffentlichen Verkehrsmitteln:
Vom Flughafen München gelangen Sie mit der S8 oder mit dem Airportbus zum Hauptbahnhof München und von dort mit dem Zug nach Augsburg Hauptbahnhof.
Vom Augsburger Hauptbahnhof nehmen Sie die Straßenbahnlinie 3 in Richtung "Haunstetten West". Die Haltestelle "BBW/Institut für Physik" befindet sich direkt vor dem Gebäude.
Anreise mit dem Auto:
Nehmen Sie auf der B17 die Ausfahrt "Messe/Universität" und biegen Sie direkt im Anschluss nach rechts in die Universitätsstraße ein. Nach ca. 1 km befindet sich rechts zwischen den Gebäuden T und R die Einfahrt in den Hertha-Sponer-Weg.
Parkplätze finden Sie entlang der beiden Gebäude R und S sowie am Ende der Straße (P9).